Recursion

Recursion is when a function calls itself(as a subroutine) until it can't, uhnnn.. A function to be considered recursive, it needs to follow two properties:

• It has to have a base case which will make it stop running infinitely
• It has to have a recursive case which will make it call itself until it reaches the base case

When we invoke functions, they get added to the Stack and once they're done running, they get removed from it. So if a recursive function doesn't have both properties, it'll be added to the Stack infinitely causing the Stack to overflow.

Here's the most famous recursive example: The Fibonacci sequece In the Fibonacci sequence each number is the sum of the two preceding ones. Say we want to calculate the Fibonacci of 3:

F(3) = F(1) + F(2)
F(1) = 1
F(2) = F(1) + F(0)
F(1) = 1
F(0) = 0

However, after reaching thee bottom, we add together every resulting number from the F function, for F(3) it is: 0 + 1 + 1 = 2, so F(3) = 2

Representing this as a tree it would look like this:

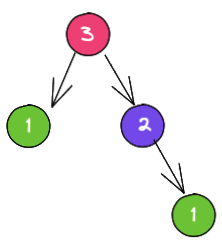
Identifying the properties from a recursive function: If we look closer, the bottom case will always be 0 or 1, so:

• base case identifies as: F(0) = 0 or F(1) = 1
• recursive case would then be n > 1: F(n) = F(n - 1) + F(n - 2)

let fib = (n: number): number => {
  if (n < 2) return n;
  return fib(n - 1) + fib(n - 2);
}

Let's make one more recursive function, this time let's reverse an array of strings:

let str  = ['o', 't', 's', 'u', 'a', 'F'];
let reverse = ([head, ...tail]: string[]): string[] => {
  if(!tail.length) return [head];
  return [...reverse(tail), head];
}

Let's analyze the above algorithm and identify the properties of a recursive function:

The way this algorithm works it that:

• It destructures the input array and takes the first element and adds it into a stack.
• Then it calls itself with all the array elements but the first one.

So, our base case happens when we call the function with an empty array and the recursive case happens when we do call the function with an array of elements.

Tail-Recursion

Tail call is a call performed as the final action of a procedure(source). If you take a look at the Fibonacci algorithm, you can see that the recursive case happens at the end of the function body:

let fib = (n: number): number => {
  if (n < 2) return n;
  return fib(n - 1) + fib(n - 2);
}

Not every recursive function is or needs to be tail-recursive, in the example above, we coul omit the return and store the result of the recursive call into a variable and do more stuff after that if we wanted to and then return whatever we wanted to.